Заметки / Плавное движение по карте высот

C++, OpenGL
 При написании программы с движением по карте высот, может потребоваться нахождение высоты точки внутри ячейки сетки ландшафта, особенно при низкой подробности карты. Это нужно для постепенного движения между высотами.


Самым простым и неточным способом будет - сложить высоты всех 4-х точек клетки и разделить на их количество. Так можно получить высоту средней точки элемента.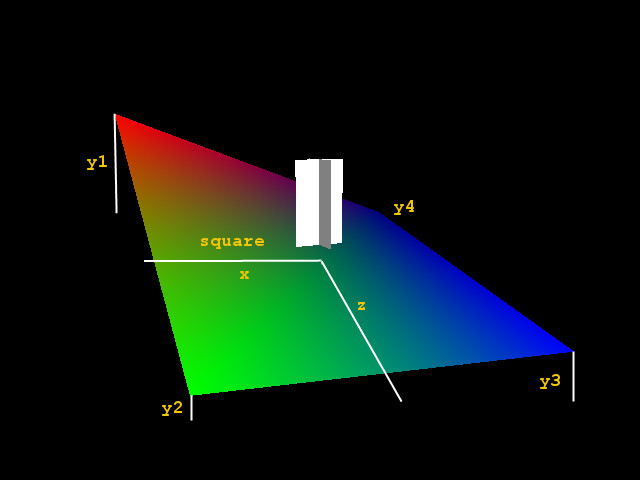 

   // Исходные данные

   // расстояние от центра до края клетки:
   float square=1.0f;
   // координаты точки:
   float x=0.0f, z=0.0f;
   // высоты углов клетки:
   float y1=1.25f, y2=0.15f, y3=0.0f, y4=0.5f;


Если развить эту формулу: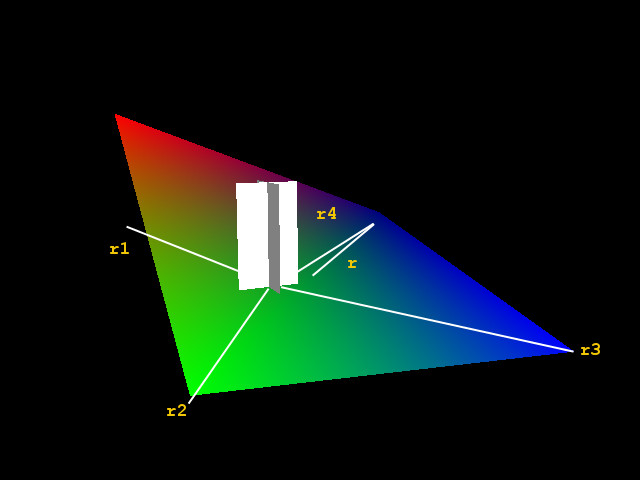 

   // 1-ый способ

   // расстояние от углов до центра:
   float r=sqrt (pow (square, 2)+pow (square, 2));
   // расстояния от каждого из углов до точки:
   float r1=sqrt (pow ((-square-x), 2)+pow ((-square-z), 2)),
         r2=sqrt (pow ((-square-x), 2)+pow ((square-z), 2)),
         r3=sqrt (pow ((square-x), 2)+pow ((square-z), 2)),
         r4=sqrt (pow ((square-x), 2)+pow ((-square-z), 2));

   // умножаем высоту на удалённость точки (чем дальше, тем меньше коэффициент)
   // и делимм на количество высот, складывая полученные значения:
   float h=(y1*(r*2-r1)/r/4.0f+y2*(r*2-r2)/r/4.0f+y3*(r*2-r3)/r/4.0f+y4*(r*2-r4)/r/4.0f);


- то она позволит вычислить любую точку плоскости (на самом деле, фигура из 4-х точек не всегда будет плоской и GL построит её в виде двух треугольников). Недостаток данного алгоритма в том, что наибольшая точность останется в центре ячейки.

Более подходящим станет такой подход: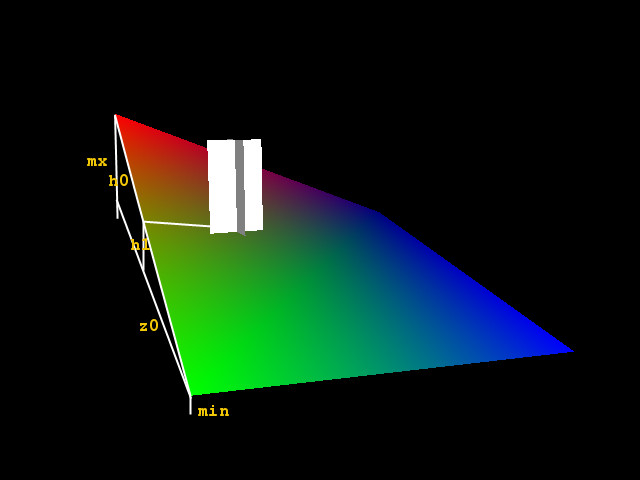 

   // 2-ой способ

   float min, mx;
   float z0, x0, h0, h1, h2;

   // берём две соседние высоты и находим бОльшую из них,
   // а также расстояние от точки до меньшей высоты на отрезке между высотами:
   if (y1>y2)
   {
    mx=y1;
    min=y2;
    z0=square-z;
   }
   else
   {
    mx=y2;
    min=y1;
    z0=square+z;
   }

   // находим разницу между высотами и получаем прямоугольный треугольник
   h0=mx-min;
   // вычисляем угол,
   float angle=atan (h0/(square*2));
   // по которому находим высоту от проекции точки на отрезок до гипотенузы между высотами;
   // к полученному значению прибавляем меньшую высоту:
   h1=tan (angle)*z0+min;
   // можно упростить и убрать atan/tan:
   h1=h0/(square*2)*z0+min;

   // повторяем вычисление для противоположного отрезка:
   if (y4>y3)
   {
    mx=y4;
    min=y3;
    z0=square-z;
   }
   else
   {
    mx=y3;
    min=y4;
    z0=square+z;
   }

   h0=mx-min;
   h2=h0/(square*2)*z0+min;

   // делаем тот же расчёт для полученных на параллельных отрезках высот:
   if (h1>h2)
   {
    mx=h1;
    min=h2;
    x0=square-x;
   }
   else
   {
    mx=h2;
    min=h1;
    x0=square+x;
   }

   h0=mx-min;
   // искомая величина - высота точки на плоскости:
   h=h0/(square*2)*x0+min;


Его можно упростить, рассчитав высоты на отрезках по пропорциям - умножив высоты на удаление (чем ближе, тем больше коэффициент) от них точки: сначала по оси Z, затем X. Похоже на первый способ, но в данном случае он работает, давая те же значения, что и предыдущий вариант.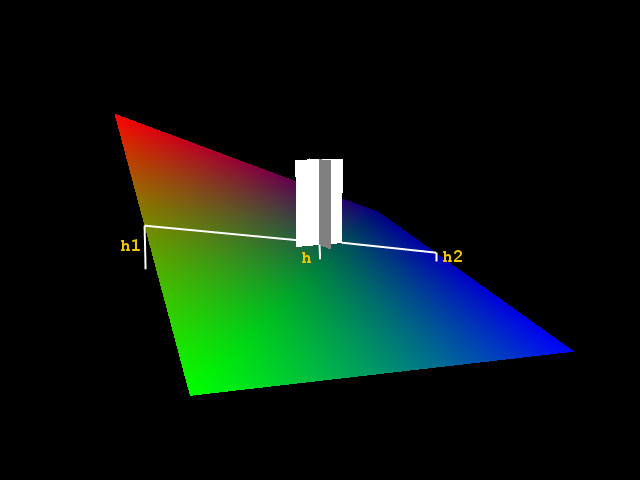 

   // Модификация 2-ого способа
   h1=y1*(square*2-(square+z))/(square*2.0f)+y2*(square*2-(square-z))/(square*2.0f);
   h2=y4*(square*2-(square+z))/(square*2.0f)+y3*(square*2-(square-z))/(square*2.0f);
   h=h1*(square*2-(square+x))/(square*2.0f)+h2*(square*2-(square-x))/(square*2.0f);


Зная высоты конечных точек прямоугольника, можно найти координаты для построения плоскости с плавным искажением поверхности. Хотя для сцены в реальном времени, это, скорее всего, лишнее - если речь не идёт о "шейдере".

Скачать полную программу.

27.07.2017